This is a short tutorial on backpropagation and its implementation in Python, C++, and Cuda. The full codes for this tutorial can be found here.

Feed Forward

Let us consider the following densely connected deep neural network

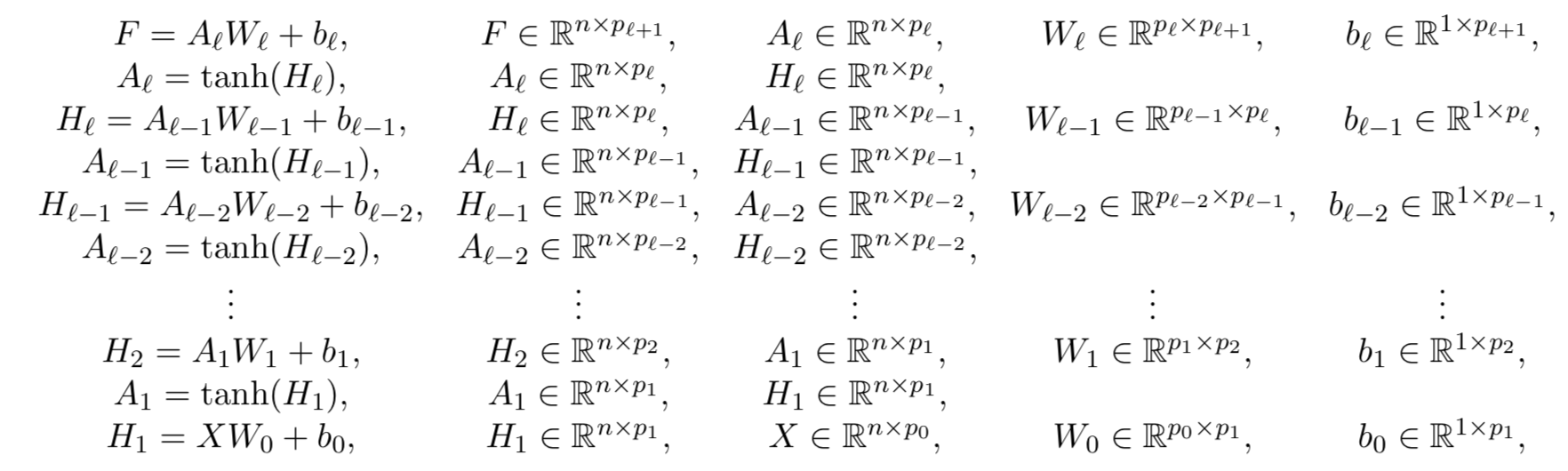
taking as input \(X \in \mathbb{R}^{n \times p_0}\) and outputting \(F \in \mathbb{R}^{n \times p_{\ell+1}}\). Here, \(n\) denotes the number of data while the weights \(W_i \in \mathbb{R}^{p_i \times p_{i+1}}\) and biases \(b_i \in \mathbb{R}^{1 \times p_{i+1}}\) represent the parameters of the neural network. Moreover, let us focus on the sum of squared errors loss function

\[\mathcal{L} := \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{p_{\ell+1}} (F_{i,j} - Y_{i,j})^2,\]

where \(Y \in \mathbb{R}^{n \times p_{\ell+1}}\) corresponds to the output data.

Back Propagation

The gradient of \(\mathcal{L}\) with respect to \(F\) is then given by

\[\begin{array}{cc} G_\ell = F - Y, & G_\ell \in \mathbb{R}^{n \times p_{\ell+1}}. \end{array}\]

Using chain rule, the gradient of \(\mathcal{L}\) with respect to \(W_\ell\) is given by

\[\frac{\partial \mathcal{L}}{\partial W_\ell} = A_\ell^T G_\ell \in \mathbb{R}^{p_\ell \times p_{\ell+1}},\]

and the gradient of \(\mathcal{L}\) with respect to \(b_\ell\) is given by

\[\frac{\partial \mathcal{L}}{\partial b_\ell} = \mathbb{1}^T G_\ell \in \mathbb{R}^{1 \times p_{\ell+1}},\]

where \(\mathbb{1} \in \mathbb{R}^{n \times 1}\) is a matrix filled with ones. The gradient of \(\mathcal{L}\) with respect to \(A_\ell\) is given by

\[\frac{\partial \mathcal{L}}{\partial A_\ell} = G_\ell W_\ell^T \in \mathbb{R}^{n \times p_{\ell}}.\]

Consequently, the gradient of \(\mathcal{L}\) with respect to \(H_\ell\), denoted by \(G_{\ell-1}\), is given by

\[G_{\ell-1} = (1 - A_\ell \odot A_\ell) \odot (G_\ell W_\ell^T) \in \mathbb{R}^{n \times p_{\ell}}.\]

Here, we are using the fact that the derivative of \(\tanh(x)\) with respect to \(x\) is given by \(1-\tanh^2(x)\). Moreover, \(\odot\) denoted the point-wise product between two matrices. The above procedure can be repeated to give us the backpropagation algorithm

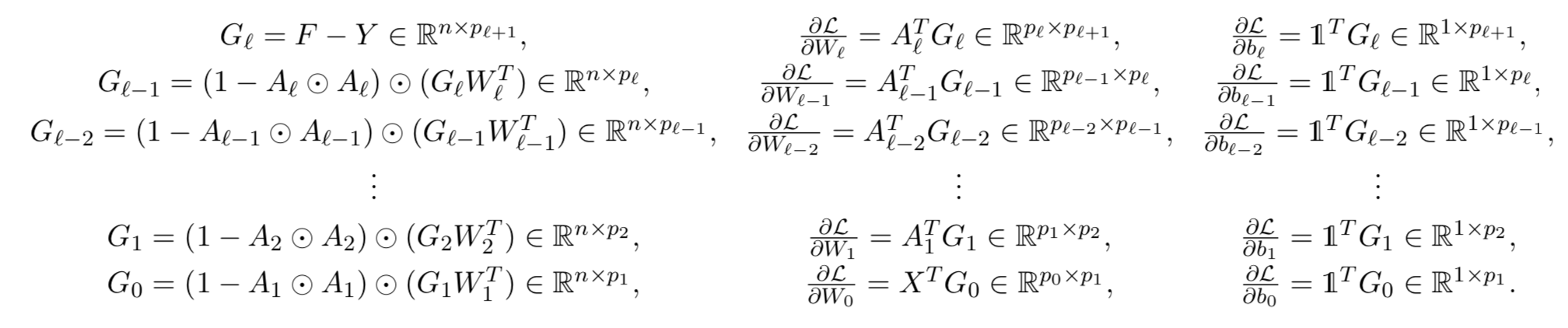
Moreover, the gradient of \(\mathcal{L}\) with respect to \(X\) is given by

\[\frac{\partial \mathcal{L}}{\partial X} = G_0 W_0^T \in \mathbb{R}^{n \times p_{0}}.\]

All data and codes are publicly available on GitHub.